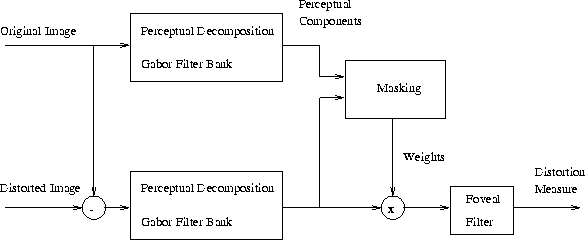
Figure 2: Schematic of the human vision model
The model [18] used here was designed for colour images and uses the opponent colour representation [13] but in this paper we restrict the discussion to monochrome images and use only the B/W channel (which is extremely close to the luminance (Y) channel). A schematic of the system is shown in Figure 2.

Figure 2: Schematic of the human vision model
Both the original image and the error are filtered into perceptual
channels. The contrast of the original image is then evaluated and
used to mask the error. This gives a distortion measure that is averaged
in a manner that crudely models the fovea.
The blocks labelled ``Perceptual decomposition'' consist of a set of
Gabor filters. The first band-pass filter in the set is isotropic
with zero response at wavenumber ![]() (to model insensitivity to global luminance level),
(to model insensitivity to global luminance level),
![]()
where k is the wavenumber measured in radians per degree of visual
of angle and ![]() rad deg
rad deg ![]() ,
, ![]() rad deg
rad deg ![]() .
.
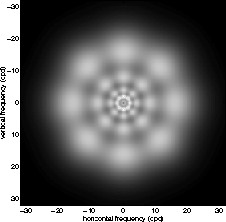
Figure 3: Response of the Gabor filter set in Fourier space. Axes are
labelled in cycles per degree of visual angle.
The other filters have a bandpass response centred on wavenumber
![]() ,
,
![]()
where ![]() ,
, ![]() . The filters,
shown in Figure 3, are chosen
to model the visual channels [8]. Each
channel of the distorted image is compared to the same channel from
the original image and a masking model applied [5].
. The filters,
shown in Figure 3, are chosen
to model the visual channels [8]. Each
channel of the distorted image is compared to the same channel from
the original image and a masking model applied [5].
The masking model used here allows only within-channel masking and uses masking weights computed as the inverse the normalised detection threshold:

where ![]() is the detection threshold
of the error in the absence of the masker. C is the error contrast
and
is the detection threshold
of the error in the absence of the masker. C is the error contrast
and ![]() is the contrast sensitivity function,
is the contrast sensitivity function,
![]()
where a=0.0192, c=1.1, d = 2.6 and ![]() rad deg
rad deg ![]() are experimentally determined constants [9].
are experimentally determined constants [9].
![]() is the contrast of the original image (the masker).
is the contrast of the original image (the masker).
The masked error contrast is averaged using a disc shaped filter. The
disc is chosen to subtend 2 ![]() so as to approximate the fovea. The
final distortion is computed as
so as to approximate the fovea. The
final distortion is computed as
where there are N channels, ![]() is the set of M pixels in
the foveal disc and e(x,y) is the masked error signal at position x, y.
The Minkowski sum in (5) is an attempt to weight errors in
the same way as human observers [18]. E(x,y) is called the Visual Difference Score.
is the set of M pixels in
the foveal disc and e(x,y) is the masked error signal at position x, y.
The Minkowski sum in (5) is an attempt to weight errors in
the same way as human observers [18]. E(x,y) is called the Visual Difference Score.