
|
Metamerism is the phenomenon whereby surfaces which, though their underlying physical properties are different, are perceived by an observer (for example, the human visual system or a colour camera) to be the same colour. Though we are not always aware of it, metamerism manifests itself in both positive and negative ways, throughout our daily lives. For example, metamerism lies at the heart of all colour reproduction. We take for granted the fact that an image of a landscape (for example the image shown in Figure 1) looks like an actual landscape: the green of the trees and the blue of the sky in the image are very close to the actual blue of the sky and the green of the real trees. That this is so however is surprising, since the physical properties of the phosphers which combine to produce the colours we observe on our monitor and the physical properties of a real tree, or the actual sky are in fact quite different. Likewise, when we print an image using a colour printer, we perceive the printed colours to be close to the actual colours of the real world objects. But again, the physical properties of the inks used to make the print are quite disimilar to the physical properties of the real objects.
Colour reproduction is an example of a situation in which metamerism has a positive impact on our daily lives. It can however sometimes have a negative effect. Consider for example the infamous ``jacket and pants'' problem. Often, when shopping for clothes we will find a jacket and a pair of trousers that appear to us to be a good colour match. Having purchased these items and taken them home however, we often discover that the two items no longer match as well as they did in the shop. It is metamerism which once more provides the explanation for this phenomenon. In this case, the physical properties of the two items are different, but when viewed under the shop lighting and due to the processes whereby we perceive colours, they nevertheless appear to match. However, when the viewing conditions change: we take the items home and look at them under a different light, the two items no longer match.
We believe that understanding the underlying processes which lead to metamerism is essential in achieving accurate colour reproduction as well as helping to avoid the problem described above. In our research we are concerned with developing a rigourous theoretical understanding of the phenomenon and in subsequently exploring the practical consequences of this theory in a range of practical applications. These pages summarise the work we have so far done in this field.
To properly understand the phenomenon of metamerism we must understand a
little about how colour is perceieved and how
a colour image is formed. An introduction to the process of colour image
formation can be found elsewhere in these pages. This model of image formation
tells us that the colour of an object is represented by the eye or a camera as a
triplet of numbers. In the case of the eye we denote
this triplet as XYZ, and as RGB in the case of a camera. Mathematically image
formation is written:
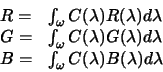 |
(1) |
These equations tell us that a visual system represents the input signal (the
colour signal
![]() , a continuous function of wavelength) by three numbers, R, G, and
B. That is,
image formation is essentially a coarse sampling of the input signal. It is
this process of sampling the input signal
that is at the heart of metamerism, for it can happen, that signals which when
represented by continuous functions
of wavelength are quite different can, after the sampling process, give rise to
the same triplet of RGB responses.
, a continuous function of wavelength) by three numbers, R, G, and
B. That is,
image formation is essentially a coarse sampling of the input signal. It is
this process of sampling the input signal
that is at the heart of metamerism, for it can happen, that signals which when
represented by continuous functions
of wavelength are quite different can, after the sampling process, give rise to
the same triplet of RGB responses.
|
As an example, consider an imaging system whose sensors respond to light
energy at only a single wavelength: the
sensors are the impulse functions illustrated in the left-hand side of Figure 2.
It follows in this case that the image formation equations
become:
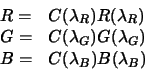 |
(2) |
So that any colour signals which share the same values at the three
wavelengths ![]() ,
, ![]() , and
, and ![]() will produce the same RGB response. In particular, all the colour signals
shown in the right of Figure 2 will produce the same response
for the narrow-band sensors. We call these colour signals metamers with
respect to one another.
Of course, in general, sensors are responsive to light at more than a single
wavelength, but in this case too, metamerism can still arise.
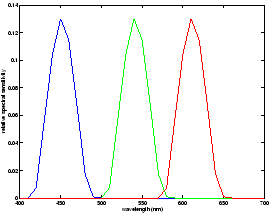
For example, the left-hand plot in Figure 3 illustrates the human visual
system's colour matching functions while the right-hand side of the same figure
illustrates a set of colour signals which are metamers with respect to these
sensors.
will produce the same RGB response. In particular, all the colour signals
shown in the right of Figure 2 will produce the same response
for the narrow-band sensors. We call these colour signals metamers with
respect to one another.
Of course, in general, sensors are responsive to light at more than a single
wavelength, but in this case too, metamerism can still arise.
For example, the left-hand plot in Figure 3 illustrates the human visual
system's colour matching functions while the right-hand side of the same figure
illustrates a set of colour signals which are metamers with respect to these
sensors.
So far we have explained metamerism in terms of two or more colour signals
which produce identical response in an imaging
device. But a colour signal is the product of two more fundamental entities:
an illuminant spectral power distribution ![]() and a surface reflectance function
and a surface reflectance function ![]() . For a fixed illuminant it
may be that there are two or more surface reflectance
functions which result in identical response for an imaging device. In this
case we say that the surfaces are metamers with
respect to one another. Now, suppose we have a set of surfaces which are
metamers when viewed under one illuminant. It is quite
possible that if the illuminant is changed the surfaces will no longer be
metameric. That is, under a different illuminant the
two surfaces produce non-identical responses in the imaging device. Indeed,
it is this that is occuring when the jacket and pants
which match in the shop fail to match when we take them home. Under the shop
illuminant the two items were metamers, but
under the different lighting our home they are no longer metameric. This
phenomenon is sometimes called illuminant metamerism.
There is too, a form of metamerism called observer metamerism. This form of
metamerism manifests itself when for example,
two or more surfaces look the same to a human observer, but produce
non-identical responses in a digital camera. This phenomenon
can arise because the light sensing properties of the two systems are not
exactly the same.
. For a fixed illuminant it
may be that there are two or more surface reflectance
functions which result in identical response for an imaging device. In this
case we say that the surfaces are metamers with
respect to one another. Now, suppose we have a set of surfaces which are
metamers when viewed under one illuminant. It is quite
possible that if the illuminant is changed the surfaces will no longer be
metameric. That is, under a different illuminant the
two surfaces produce non-identical responses in the imaging device. Indeed,
it is this that is occuring when the jacket and pants
which match in the shop fail to match when we take them home. Under the shop
illuminant the two items were metamers, but
under the different lighting our home they are no longer metameric. This
phenomenon is sometimes called illuminant metamerism.
There is too, a form of metamerism called observer metamerism. This form of
metamerism manifests itself when for example,
two or more surfaces look the same to a human observer, but produce
non-identical responses in a digital camera. This phenomenon
can arise because the light sensing properties of the two systems are not
exactly the same.
The existence of metamerism implies that there is a fundamental ambiguity in our visual perception. Given a triplet of cone responses: the eye's response to light from some surface, it is not possible for us to uniquely identify the physical properties of that surface but rather, there exist many surfaces consistent with the response. In the Colour Group at UEA we are trying to better understand the phenomenon of metamerism and to explore the implications it has for our own visual system and also for such tasks as colour reproduction and computer vision.
The starting point for our work is to answer the following question. Given a triplet of cone responses, or an RGB from a device, what are the possible surfaces which could have produced this response? That is, we would like to recover all surface reflectance functions which produce a given response. As discussed above however, surfaces which are metameric under one illuminant need not be metameric when the light changes. And equally, surfaces metameric for one observer, may not be metamers for an observer with different sensor properties. In light of this we set out to answer the question: Given an RGB observed under an illuminant of known spectral power distribution, by a device of known sensor sensitivities, what are the surfaces that would produce this response?
To answer the question we go back to the colour image formation equations
(Equation 1) given above. We can write
these equations in vector matrix notation as:
| (3) |
| (4) |
In our case we know the sensor response ![]() and the lighting
matrix
and the lighting
matrix ![]() and we would like to determine
and we would like to determine
![]() . In mathematical terms Equation (4) is a set of three linear equations in
n unknowns (n is the number of samples we use
to represent our surface). In general n » 3, so that Equation (4) is
under-constrained: there are more unknowns than there
are equations. The laws of linear algebra tell us that for such
under-constrained systems there exists not a unique solution but rather an
infinite set of possible solutions. This is consistent with what we have said
so far about metamerism
since we have said that there can exist many surfaces which produce identical
response for a given observer and illuminant. Equation (4)
expresses the same thing in mathematical form.
. In mathematical terms Equation (4) is a set of three linear equations in
n unknowns (n is the number of samples we use
to represent our surface). In general n » 3, so that Equation (4) is
under-constrained: there are more unknowns than there
are equations. The laws of linear algebra tell us that for such
under-constrained systems there exists not a unique solution but rather an
infinite set of possible solutions. This is consistent with what we have said
so far about metamerism
since we have said that there can exist many surfaces which produce identical
response for a given observer and illuminant. Equation (4)
expresses the same thing in mathematical form.
It follows that to determine the set of surfaces consistent with a given
response we must solve Equation (4) to recover the
set of possible reflectances. We call this set the Metamer Set and we solve
for it using the rules of linear algebra together
with some additional constraints which exploit what knowledge we have about
the nature of surface reflectance functions.
Linear algebra tells us that any solution to Equation () can be decomposed
into two parts: a particular solution which
we denote ![]() and which is a reflectance satisfying Equation (4), and a
solution to the corresponding homogeneous equation:
and which is a reflectance satisfying Equation (4), and a
solution to the corresponding homogeneous equation:
| (5) |
which we denote ![]() . Any solution to Equation (4) can be written:
. Any solution to Equation (4) can be written:
| (6) |
where ![]() is an arbitrary scale factor. So our strategy for determining
the set of possible surface reflectances is to find
a particular solution to Equation (4) and to then find solutions to the
associated homogeneous equation. These two completely
determine the set of possible solutions. However, because of the nature of our
problem we can further constrain our solution
set by exploiting the particular properties of surface reflectance functions.
In particular, we know that a surface can reflect no
less than zero light, nor no more than all light that is incident upon it. So
that any solution to our system must satisfy the
following two linear constraints:
is an arbitrary scale factor. So our strategy for determining
the set of possible surface reflectances is to find
a particular solution to Equation (4) and to then find solutions to the
associated homogeneous equation. These two completely
determine the set of possible solutions. However, because of the nature of our
problem we can further constrain our solution
set by exploiting the particular properties of surface reflectance functions.
In particular, we know that a surface can reflect no
less than zero light, nor no more than all light that is incident upon it. So
that any solution to our system must satisfy the
following two linear constraints:
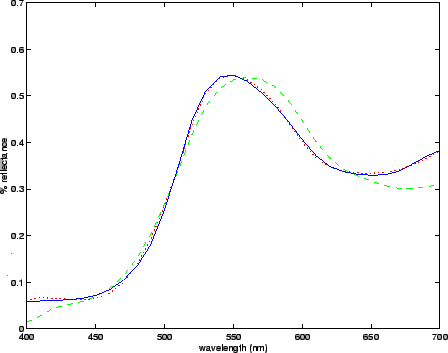
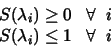 |
(7) |
That is, reflectances must be everywhere greater than zero and less than one. In addition, an analysis of sets of real measured reflectances reveals that they are not arbitrary functions but that they share a large degree of commonality. By this we mean that all reflectances are alike in some sense. In mathematical terms our reflectances are points in an n-dimensional space and they are alike in the sense that these points are not spread uniformly throughout space but rather are located in a fixed region, or sub-space of the space.
Work in the group has shown how to solve for the whole set of surfaces metameric with respect to a given response by incorporating the rules of linear algebra together with constraints on the nature of real reflectances. Full details of the metamer set solution can be found in [5].
The Metamer Set theory deepens our understanding of metamerism and it also turns out to be a powerful entity which aids in the study of both metamerism, and other problems in colour science. In particular we have used the Metamer Set theory to study a number of properties of metamers which have been previously investigated in the literature.
It has long been known that for two surface reflectance functions to be metamers with respect to the human visual system they must cross at least 3 times throughout the visible spectrum. With this in mind researchers have asked whether there is anything special about these crossover wavelengths: are there particular wavelengths where metamers cross, or are they as likely to cross at one wavelength as at another. Prior to our work, a number of authors [15,11,10,1] have investigated where, statistically, metamers cross. Their investigations have typically been based on only a few metamers and the results are inconclusive.
|
The Metamer Set theory provides us with all metamers with respect to a given response and thus we are able to use the theory to investigate metamer crossover wavelengths. To this end we conducted a statistical analysis of metamer crossovers to determine an estimate of the probability that metamers cross at any given wavelength. A full description of this work and its results can be found in [6]. Figure 4 shows typical results. It shows that there are three clear peaks corresponding to three wavelengths where it is statistically likely that metamers will cross. Significantly these peaks correspond to wavelengths 450nm, 540nm, and 610nm, which are often referred to as the prime wavelengths. These prime wavelengths arise in a variety of other studies of other phenomena [3] and it is thought that they have some special significance for the human visual system. Our studies of metamer crossovers support this belief.
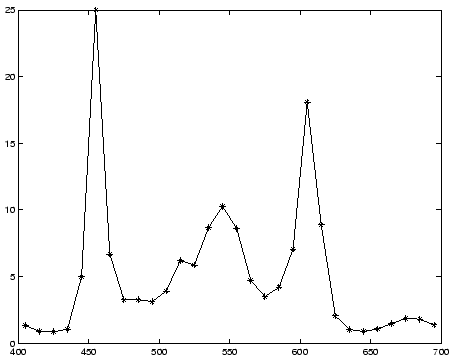
Another problem which we have investigated using Metamer Set theory is the question as to how likely it is that we will observe a given sensor response. In the context of Metamer Set Theory we approach the problem from the perspective of asking how many metamers exist for a given sensor response. The answer of course, is that there are (with certain exceptions) infinitely many metamers corresponding to each sensor response. The Metamer Set is a closed region of reflectance space and since the space is continuous there are infinitely many reflectances in the metamer set. However, it is the case that the volume of the metamer set varies according to the corresponding sensor response. For example, the metamer set for a neutral surface is relatively large, whilst as colours become more saturated the metamer set volume decreases. In the limiting case of a monochromatic reflectance (a surface which reflects light at only a single wavelength) the metamer set is a single point and its volume is zero since there are no surfaces metameric to such a reflectance.
|
Figure 5 illustrates how the volume of metamer sets changes as we move
throughout colour space. Here we show the relative volumes of
the metamer sets for all colours represented in a 2-d chromaticity space. That
is, sensor responses are projected to 2-dimensional co-ordinates
![]() such that intensity information is ignored. The metamer set theory
allows us to study such problems as chromaticity mismatch volumes and
has possible application to the colour constancy or illuminant estimation
problem which is discussed elsewhere on these pages.
such that intensity information is ignored. The metamer set theory
allows us to study such problems as chromaticity mismatch volumes and
has possible application to the colour constancy or illuminant estimation
problem which is discussed elsewhere on these pages.
In addition to allowing us to study the problems outlined above, the Metamer Set theory can also help in solving some practical problems in colour science and colour reproduction. For example, we are currently investigating how the metamer set theory can help in the problems of surface reflectance estimation and colour correction.
Reflectance estimation is the problem of determining the underlying surface reflectance function corresponding to a given response recorded by some imaging device. It is exactly this problem that we set out to solve using the Metamer Set approach. More traditionally, researchers [8,2,12,13,14,9] have ignored the problem of metamerism when estimating reflectance and have instead made certain simplifying assumptions so as to recover a single surface reflectance corresponding to a recorded response.
|
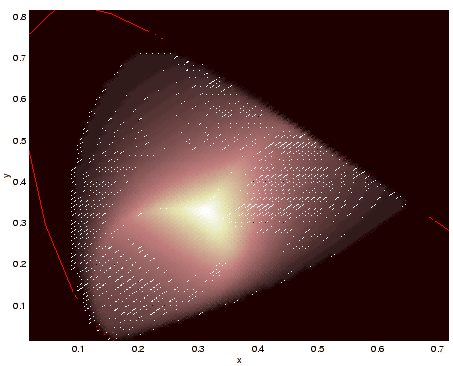
Using the metamer set approach we recover first the set of all reflectances consistent with a recorded response and only then select a single reflectance from this set. This affords a number of important advantages: the estimated reflectance is guaranteed to be a real reflectance (in the sense that it is physically realiseable) and in addition, the metamer set gives us a measure of uncertainty or possible error in our estimate. Existing reflectance estimation methods offer neither of these properties. Figure 6 illustrates the typical performance of our estimation method. From the actual reflectance (shown in blue in this Figure) we generated a camera RGB response and then used metamer set reflectance estimation to recover an estimate of the reflectance from the response. The red curve shows the recovered reflectance. While current estimation performance is quite good we are currently investigating ways to further improve estimation performance.
In colour reproduction it is common that we take an image recorded with, for example a digital camera, and display it on a CRT monitor or print it using a laser or inkjet printer and finally look at it with our own eyes. An important issue in this reproduction process is the fact that each device or imaging system has its own representation of ``colour''. As we have seen, a camera records light as an RGB triplet corresponding to the responses of its sensors, while for the human visual system, colours are, to a first approximation, represented by XYZ values. It is important therefore that we are able to transform from one colour space to another, a process which is often referred to as colour correction.
There exist many suggestions [4,8,16,7] as to how best to transform from one colour space to another, but to date few researchers have considered the issue of metamerism in this context. In practice however, metamerism is fundamental to the colour correction problem. We have seen that for a given XYZ response recorded say by our own visual system, there exists a set of surface reflectance functions which are consistent with this response. Suppose now that we image all these reflectance functions with a digital camera. It follows that because a camera senses light differently to our own eye, there is no guarantee that these surfaces will look the same to the camera. That is, metamers with respect to our own visual system need not be metameric for the camera. It follows then that the transformation from XYZ to RGB is a one-to-many mapping; each XYZ can potentially map to an infinity of RGBs.
Importantly, the metamer set theory enables us to determine the set of possible RGBs corresponding to a given XYZ. Simply, we recover first the set of reflectances, metamers to our XYZ and then calculate the corresponding RGBs for a given device. To complete the colour correction process we simply select an RGB from amongst this set. We have shown that taking this approach leads to improved colour correction and we are currently investigating how the metamer set theory can be further exploited to obtain even greater improvements.