
|
As we walk through the world, interacting with objects, we take for granted the fact that for the most part, the colour of those objects is unchanging; the pages of a book appear to us white, whether we view them inside under a yellowish tungsten light, or outside under a blue sky illuminant. This property of our colour perception is quite surprising when we consider the process of image formation. An overview of colour image formation is given here. Essentially, colour perception arises from the interpretation by our eye and brain of light incident upon the eye. Typically this incident light is the reflection of light from the surface of an object. For example light from the sun is reflected from an object and the reflected light enters our eye. The energy emitting properties of different light sources is quite different as illustrated by Figure 1 which shows the spectral power distribution of a tungsten filament light and that of the light outside on a clear sunny day. As a consequence of this difference, the input to our visual system changes according to the prevailing illumination conditions: the light reflected from an apple is different depending on whether we look at it inside under the tungsten light or outside under daylight. Nevertheless, our visual system is able to compute from this changing signal, a perception of an object which is stable. It is this ability of a visual system that we refer to when we talk about colour constancy.

|
The fact that colour constancy is a non-trivial property of a visual system can be made clear by considering a camera's response to objects under two different illuminants. Figure 2 shows two images of the raw camera output from a typical digital still camera. In the left-hand image the scene was imaged under a tungsten illumination while the image on the right-hand was taken under a daylight simulator. There is a clear shift in colour between these two images: the colours in the scene lit by the reddish tungsten illuminant appear generally redder than those lit by the bluish daylight illuminant.

|
Colour constancy is a useful property for any visual system performing tasks which require a stable perception of an object's colour. In our own visual system colour helps us to identify objects, a task which would become much more difficult were the colour of an object to change depending on the prevailing illumination conditions. Computer vision researchers too [19] would like to identify objects simply by comparing the colour distributions of images of those objects. However, it is clear from Figure 2 that this task will be impossible unless account is taken of the light under which an image is captured.
Colour constancy is also important in the context of image reproduction. When we look at a scene, our own visual system corrects the colours to account for the scene illumination, but as we see in Figure 2, by default a digital camera does not. This implies that if we look at an uncorrected image of a scene taken with such a camera, the uncorrected colours will appear wrong to us. Thus, for the accurate reproduction of colour images, we must correct images recorded with a digital camera to account for the colour of the prevailing light. In practice solving this problem amounts to accurately estimating the colour of the illumination in a scene. Figure 3 illustrates the importance of correctly estimating the scene illumination. The left-hand image shows a colour reproduction based on an accurate estimate of the scene illumination while the right-hand image shows a reproduction when the scene illumination is poorly estimated. In the Colour Group we have conducted considerable research into the problem of accurate illuminant estimation. Below we discuss the problem in more detail and give an overview of our solutions to it.

|
The problem of Colour Constancy has been long studied by (both human and computer) vision researchers [16,17,5,6,3,4,18,20,15,7,13,9,8], in an attempt both to understand how our own visual system achieves colour constancy and also to develop algorithms to provide cameras with this same ability. To understand such algorithms and their design it is helpful to clarify our definition of the problem at hand. To this end, it is useful to consider the process of image formation. For an introduction to image formation the reader is referred to here. In mathematical terms image formation can be written:
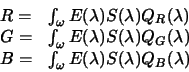 |
(1) |
Equation 1 tells us that a visual system's responses (the R, G, and B values) depend on
three underlying physical entities: the spectral power distribution of the illuminant
![]() , the surface reflectance function
, the surface reflectance function ![]() , and the spectral response
functions (
, and the spectral response
functions (![]() ,
, ![]() , and
, and ![]() ) of the visual system. In
the context of colour constancy it
is the dependence on
) of the visual system. In
the context of colour constancy it
is the dependence on ![]() that interests us most. For suppose that surface and
sensor response are fixed, but that
that interests us most. For suppose that surface and
sensor response are fixed, but that ![]() is allowed to change. It follows that an imaging
system will record a response to a surface which changes according to the change in
is allowed to change. It follows that an imaging
system will record a response to a surface which changes according to the change in ![]() .
This then is the explanation as to why the images in Figure 2 are differently coloured.
.
This then is the explanation as to why the images in Figure 2 are differently coloured.
The question then is how we can make those image colours constant, regardless of the
prevailing illumination? The answer is that we must apply some kind of correction to
the colour responses to account for the nature of the scene illuminant. Clearly, the
correction we apply must depend on the scene illuminant and so as a first step in solving
this problem we might try to estimate the illuminant ![]() . Indeed, it turns out that if
we know the illuminant spectrum, then it is relatively straightforward to apply a
correction to sensor responses to account for it. But very often the scene illuminant
is unknown and so it must be estimated from just the image data.
. Indeed, it turns out that if
we know the illuminant spectrum, then it is relatively straightforward to apply a
correction to sensor responses to account for it. But very often the scene illuminant
is unknown and so it must be estimated from just the image data.
An examination of Equation 1 reveals that this is not an easy problem to solve. To see why, suppose we have an RGB sensor response to a single surface. Equation 1 tells us that this response depends on three factors - light, surface, and sensor. It may be that we know something about the sensor, which leaves only light and surface unknown. However, both these quantities are continuous functions of wavelength, whereas what we measure at each pixel are only three discrete samples of light multiplied by surfaces. At a pixel then, we have insufficient data to properly recover light and surface. Of course, more surfaces (that is, different pixel responses) add more information about the light but at the cost of introducing more unknowns - the underlying properties of the new surfaces. In general, regardless of how many surfaces we look at, we will always have more unknown quantities than we have data and thus the problem cannot be solved in this way.
Fortunately, obtaining an estimate of ![]() is unnecessary in many cases.
In fact what we would really like to know is, given a response (or set of responses)
recorded under an unknown illuminant
is unnecessary in many cases.
In fact what we would really like to know is, given a response (or set of responses)
recorded under an unknown illuminant ![]() , what would the corresponding responses have
been under a different light
, what would the corresponding responses have
been under a different light ![]() . That is, we would like to know how to map the colours we
observe under some arbitrary light to a reference light. Provided that we can reliably
determine such a mapping then our own or a camera's visual system will be colour
constant. This problem is easier to solve than estimating
. That is, we would like to know how to map the colours we
observe under some arbitrary light to a reference light. Provided that we can reliably
determine such a mapping then our own or a camera's visual system will be colour
constant. This problem is easier to solve than estimating ![]() directly because it turns
out that sensor responses to a surface under two different lights are often related by
quite a simple mapping. However, even though the form of the mapping is simple,
there does not yet exist an algorithm capable of reliably determining the mapping for an
arbitrary image.
directly because it turns
out that sensor responses to a surface under two different lights are often related by
quite a simple mapping. However, even though the form of the mapping is simple,
there does not yet exist an algorithm capable of reliably determining the mapping for an
arbitrary image.
In the Colour Group we have conducted considerable research into the colour constancy/illuminant estimation problem. Some of this research is discussed further in these pages.
Solving the illuminant estimation problem in the form outlined above depends crucially on the nature of the mapping between sensor responses under different illuminants. One model of illuminant change that has been proposed (explicitly and implicitly) many times in the literature [16,15,10] is the so called diagonal model sometimes also called the von Kries model after the researcher who first proposed it. Mathematically this model is simple:
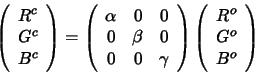 |
(2) |
Equation 2 tells us that the responses to a surface imaged under two different
illuminants are related by three simple scale factors. So, when the illumination
changes, all red responses change by a factor ![]() , all green by a factor
, all green by a factor
![]() and all blue by a factor
and all blue by a factor ![]() . Whether or not such a model is an
appropriate one depends to a large extent on the sensors of the visual system
under consideration. Fortunately Equation 2 is a
reasonably accurate model for a large class of image sensors and the method of
spectral sharpening (discussed elsewhere in these pages) broadens the range of
sensors for which the model is valid.
. Whether or not such a model is an
appropriate one depends to a large extent on the sensors of the visual system
under consideration. Fortunately Equation 2 is a
reasonably accurate model for a large class of image sensors and the method of
spectral sharpening (discussed elsewhere in these pages) broadens the range of
sensors for which the model is valid.
Adopting the model in Equation 2 the illuminant
estimation problem becomes that of determining the three scale factors ![]() and
and
![]() required to map responses under light
required to map responses under light ![]() to those under light
to those under light ![]() .
David Forsyth [14,15] was the first researcher to
formally state the problem in this form and importantly, he also realised that
for a typical image, there is no unique answer to this question. That is,
given only a set of sensor responses recorded under illuminant
.
David Forsyth [14,15] was the first researcher to
formally state the problem in this form and importantly, he also realised that
for a typical image, there is no unique answer to this question. That is,
given only a set of sensor responses recorded under illuminant ![]() ,
there are many mappings which give a set of responses consistent with a set
of surfaces viewed under illuminant
,
there are many mappings which give a set of responses consistent with a set
of surfaces viewed under illuminant ![]() .
.
Forsyth's approach was to find the set of all possible mappings consistent with a set of image data, and to then choose a single mapping from amongst these. Forsyth's work has been since been significantly improved by researchers in the Colour Group [7,11,12,13] and others [1,2]. We outline the contribution made by the colour group below.
The first step in Gamut Mapping colour constancy is to define a standard, or canonical illuminant, and to then define the gamut of colours which it is possible to observe under this light. Forsyth defined this gamut in 3-dimensional RGB space and showed that it in this space the gamut is a bounded convex object. Later, Finlayson [7] suggested that it is better to instead represent the gamut (and colours in general) in a 2-dimensional chromaticity space. He suggested the space given by the following equation:
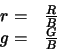 |
(3) |
In chromaticity space the intensity or overall brightness of a colour is discarded whilst retaining the chromatic content of the colour. The particular space defined by Equation 3 has the additional useful property that if RGBs under different illuminants are related by a diagonal transform so to are the corresponding chromaticity co-ordinates.
The fact that the gamut is bounded is important in that it tells us that not all colours can be observed under a given light. From this fact it follows that the colours we observe in an image tell us something about the light in the scene. For example, observing a colour outside the gamut of the canonical illuminant tells us that the light was something other than the canonical.
To see how the gamut mapping algorithm works, suppose that the canonical gamut
of image chromaticities can be represented by the triangle in the top left of
Figure 4. Now, suppose further that we have an image consisting of three
chromaticities labelled ![]() ,
, ![]() , and
, and ![]() shown in the top right of Figure 4.
Each of these chromaticities represents a different surface and in solving
for colour constancy we are essentially trying to find the
chromaticities under the canonical light corresponding to these surfaces. To
help us do this we make the assumption that the observed chromaticities and the
corresponding canonical chromaticities are related by a diagonal transform.
However, if we consider the single chromaticity
shown in the top right of Figure 4.
Each of these chromaticities represents a different surface and in solving
for colour constancy we are essentially trying to find the
chromaticities under the canonical light corresponding to these surfaces. To
help us do this we make the assumption that the observed chromaticities and the
corresponding canonical chromaticities are related by a diagonal transform.
However, if we consider the single chromaticity ![]() , there are many diagonal
transforms which map it into the canonical gamut.
, there are many diagonal
transforms which map it into the canonical gamut.
In fact we can map ![]() to any point inside the gamut by a diagonal transform.
So, there exists a set of diagonal transforms mapping
to any point inside the gamut by a diagonal transform.
So, there exists a set of diagonal transforms mapping ![]() into the gamut.
We can represent these transforms in a 2-d space too - they are represented
by the blue polygon in the bottom of Figure 4.
Now, suppose we take a second chromaticity
into the gamut.
We can represent these transforms in a 2-d space too - they are represented
by the blue polygon in the bottom of Figure 4.
Now, suppose we take a second chromaticity ![]() and try to map it into the
canonical gamut. Again there are a set of possible mappings from
and try to map it into the
canonical gamut. Again there are a set of possible mappings from ![]() to this gamut a set which we illustrate
by the green polygon in Figure 4. Importantly, the green and blue polygons
intersect. This tells us that there exist some mappings which take both
to this gamut a set which we illustrate
by the green polygon in Figure 4. Importantly, the green and blue polygons
intersect. This tells us that there exist some mappings which take both
![]() and
and ![]() into the canonical gamut. Thus, given the two points
the intersection region defines the set of possible mappings and effectively
the possible scene illuminants. If we have a third chromaticity (
into the canonical gamut. Thus, given the two points
the intersection region defines the set of possible mappings and effectively
the possible scene illuminants. If we have a third chromaticity (![]() for
example), it too has an associated
set of plausible mappings (the red polygon), and once again we can intersect
this set with the mappings for
for
example), it too has an associated
set of plausible mappings (the red polygon), and once again we can intersect
this set with the mappings for ![]() and
and ![]() to give us the set
of plausible mappings. By repeating this process for all colours in an image
we arrive at a set of mappings consistent with the image data.
to give us the set
of plausible mappings. By repeating this process for all colours in an image
we arrive at a set of mappings consistent with the image data.
To complete the process we must select one mapping from this set as our estimate of the illuminant. Unfortunately, Finlayson [7] found that the mappings in this set need not correspond to illuminants which are plausible in the world. That is, while the method gives us all mappings consistent with the image data, not all mappings correspond to an illuminant which we will encounter in the real world. Finlayson argued that by exploiting knowledge of real world illuminants we can further improve on the Gamut Mapping solution. For example, the top left of Figure 5 shows mappings corresponding to a large set of real world illuminants. By intersecting this set of mappings with the set of mappings we get from our image data (top right of Figure 5) we arrive at a set of mappings that are both consistent with our image data and correspond to actual illuminants (bottom of Figure 5). It still remains to choose a single mapping from this set to be our illuminant estimate and, as our [11,12,13] (and others [1,2]) research has shown, how this choice is made can have a considerable effect on algorithm performance.
With a careful selection procedure, the gamut mapping algorithm can give very good colour constancy, but it is not perfect and there are a number of limitations of the approach. Chief amongst these is the fact that the algorithm is non-trivial to implement and computationally complex. In addition, the reliance of the approach on a diagonal model of illumination change sometimes means that the algorithm gives no illuminant estimate. In the Colour Group we are attempting to overcome these limitations, both by further developing the gamut mapping method and by exploring different approaches to the problem.
A different approach to illuminant estimation which we have developed within the Colour Group is a method which we call Colour By Correlation. This method has been developed in conjunction with researchers at Hewlett-Packard Laboratories and shows great promise. Indeed, a version of the algorithm was included by Hewlett-Packard in the image processing pipeline of their Photosmart digital cameras. An overview of the theory of colour by correlation is given below.
Colour by Correlation builds on the gamut mapping approach described above, developing that work in a number of significant ways. First, we develop a computational framework in which it is possible re-formulate the gamut mapping approach. Importantly, illuminant estimation within the new framework is robust and computationally simple. In addition the new framework allows us to incorporate probabilistic information on the likelihood of observing different image colours under a given illuminant, information which significantly improves estimation performance.
Colour By Correlation can best be described as an illuminant
classification algorithm. We begin by describing a priori a discrete set
of possible scene illuminants.
Suppose for example that we limit our set of possible illuminants to just two:
daylight and tungsten filament. For each of these illuminants we can determine
the gamut of image colours which can be observed under each. Figure 6
illustrates the gamuts for the two lights in a 2-d chromaticity space. We can
usefully code this chromaticity space into three regions which we label
![]() ,
, ![]() , and
, and ![]() . Region
. Region ![]() represents colours
which can be observed under only daylight, region
represents colours
which can be observed under only daylight, region ![]() , those colours
seen only under Tungsten, and region
, those colours
seen only under Tungsten, and region ![]() contains colours we might see
under either light. This information can in turn be coded in a table such as
that illustrated in the bottom of Figure 6. Each column of this table
corresponds to one of the two lights and each row to one of the three regions
of chromaticity space. A one in a table entry means that chromaticities in the
corresponding region might be observed under the corresponding light, otherwise the table entry is zero.
contains colours we might see
under either light. This information can in turn be coded in a table such as
that illustrated in the bottom of Figure 6. Each column of this table
corresponds to one of the two lights and each row to one of the three regions
of chromaticity space. A one in a table entry means that chromaticities in the
corresponding region might be observed under the corresponding light, otherwise the table entry is zero.
Now suppose we wish to classify the scene illuminant for a simple image. First
we determine which image colours (chromaticities) are present in the image.
Supposing that the image contains chromaticities in region ![]() and
and
![]() what does this tell us about the scene illuminant? A chromaticity in
region
what does this tell us about the scene illuminant? A chromaticity in
region ![]() is consistent with only daylight illumination and so this
chromaticity is a ``vote'' for that light. Region
is consistent with only daylight illumination and so this
chromaticity is a ``vote'' for that light. Region ![]() is consistent with
both lights so that a chromaticity in that region votes for both lights. In
total then we have two votes for daylight and a single vote for Tungsten and
on the basis of this information we might conclude that the illumination was
daylight.
is consistent with
both lights so that a chromaticity in that region votes for both lights. In
total then we have two votes for daylight and a single vote for Tungsten and
on the basis of this information we might conclude that the illumination was
daylight.
This simple example captures the essence of the Colour by Correlation algorithm. In practice our scene illuminant could be more than just daylight or Tungsten, but to allow for more possiblities we need simply add more columns to our table. Similarly, we will need to divide the chromaticity space into more than just three regions, but we can represent as many regions as we need by simply adding more rows to the table. We can then classify an image by following the voting procedure outlined above.
We can also express this voting procedure mathematically. First, we code
the information in our table as a matrix ![]() with the entries of
with the entries of ![]() corresponding to entries in the table. We call this matrix
corresponding to entries in the table. We call this matrix ![]() a correlation matrix. Next we can represent the colours
(chromaticities) in an image in a vector
a correlation matrix. Next we can represent the colours
(chromaticities) in an image in a vector ![]() . Each element of
. Each element of
![]() corresponds to a region of chromaticity space and the element of
the vector will contain a one if its corresponding chromaticity is present in
the image, otherwise it will be zero. To calculate the votes for each illuminant
is then simply:
corresponds to a region of chromaticity space and the element of
the vector will contain a one if its corresponding chromaticity is present in
the image, otherwise it will be zero. To calculate the votes for each illuminant
is then simply:
| (4) |
The algorithm just outlined represents a simple framework for illuminant estimation. As described it shares a number of similarities with the gamut mapping approach described above - most significantly it uses constraints on the gamut of possible image colours to obtain information about the illumination in a particular scene. But formulating the solution in this framework we can also go a step further and ask, what is the likelihood of observing a given image colour under each of the possible scene lights. That is, for each light we can determine a probability distribution, by the process illustrated in Figure 7,
The bottom left of Figure 7 shows the distribution of 2-dimensional image
chromaticities under a standard daylight illuminant. Importantly, the figure
tells us that under this light we are much more likely to observe some
chromaticities than others. In addition, image chromaticities are distributed
differently under a different
lights. We can determine a chromaticity distribution for each illuminant and
represent each distribution as a column of a correlation matrix. Once
established, this probabilistic correlation matrix can be used exactly as
described above. The only change is that now, rather than
defining a correlation matrix whose entries are one or zero, a matrix entry
will tell us something about the probability of observing the corresponding image
colour under the relevant light. In mathematical terms the ![]() th column of the
correlation matrix is related to the conditional probability distribution
th column of the
correlation matrix is related to the conditional probability distribution
![]() - the probability of observing each
chromaticity given that the illuminant is
- the probability of observing each
chromaticity given that the illuminant is ![]() . To estimate the illuminant we
would like to determine a different probability distribution:
. To estimate the illuminant we
would like to determine a different probability distribution:
![]() : the probability that the illuminant is
: the probability that the illuminant is ![]() given the chromaticities we observe. Bayes rule tells us how these two
probabilities are related:
given the chromaticities we observe. Bayes rule tells us how these two
probabilities are related:
| (5) |
For an image the denominator of this fraction is fixed, and if we assume that
all possible illuminants occur with equal likelihood then we have the following
relationship:
| (6) |
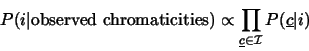 |
(7) |
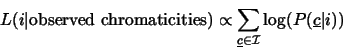 |
(8) |
| (9) |
Employing probabilistic information rather than simple chromaticity gamuts leads to a significant performance in algorithm performance. In general the correlation approach to illuminant estimation has proven to give excellent colour constancy performance. Work is ongoing in the Colour Group to improve its performance further. For example, how we measure the likelihood of observing a given image colour under each illuminant has a significant effect on algorithm performance. We are currently investigating different approaches to this issue.