|
Physics based vision is about interpreting an image and extracting information about its contents based on an understanding of the underlying physics which govern how the image was formed. Our work in this area has concentrated on one particular problem: that of illuminant estimation. Estimating the prevailing illumination in a scene given only an image of the scene is a much studied problem and one that we have studied from a number of different perspectives. In this work we start from a a particular physical model of image formation called the dichromatic model which was first proposed by Shafer et al [9].
|
|
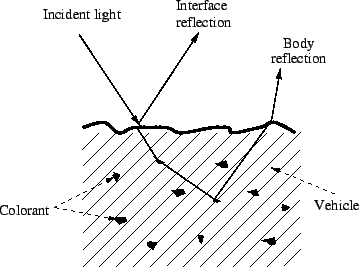
In simple terms the dichromatic model of image formation says that light is
reflected from a surface is reflected in one of
two ways, as illustrated in Figure 1. The first type of reflection is known as
surface reflection and refers to the case in which the
surface acts like a mirror and simply reflects any light which is incident
upon it. In this case the light does not interact
with the surface in any way and thus the reflected light is spectrally the
same as the incident light. The second type of reflection
is referred to as body reflection and in this case light enters the surface
where it is selectively absorbed and emitted by
colorant particles within the body of a material before eventually leaving the
surface at some point. The process of body reflection
spectrally alters the incident light so that the reflected light depends on
properties of the surface as well as the incident light.
Light reflected by the body process can be reflected in any direction whereas
surface reflected light is reflected in a single
direction. Any light, however it arises, can be characterised by its spectral
power distribution (SPD) which is a continuous function
of wavelength. If we adopt the dichromatic model of reflection then the light
reflected from a point on a
surface consists of a linear combination of two distinct lights: body
reflected light 
and surface reflected light
. That is:
 |
(1) |
Now suppose that an image is formed by a trichromatic camera with linear
response. It follows that the 
recorded
by the camera for the light 
can be expressed as the same linear
combination of two s:
 |
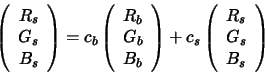(2) |
Equation 2 is useful because it splits out that part of the which
depends on the surface (
) and the part
which depends only on the incident light (
). In the context of
illuminant estimation, it is this quantity which
we would like to determine and Equation 2 provides the first step towards
obtaining it.
Suppose we consider all pixels corresponding to a single surface. By the
analysis above we know that the of any such
pixel consists of two constituent s corresponding to body and surface
reflected light. Pixel values for different points
on this surface can differ because the relative amounts of body and surface
reflected light they contain can differ. But what
Equation 2 tells us is that all pixels for this surface must fall on a plane
in space and that this plane is spanned by two vectors
: the body and the surface . Consider also the pixels on a second,
distinct surface. These pixels two must also
fall on a plane in space though the plane will be different to that of
the first. However, these two planes share
something in common: one vector which is in their span is ()
which is the corresponding to
the prevailing illumination. In fact, the two planes must intersect at a line
and this line of intersection is exactly the line in the
direction of (). Thus we have a simple method of determining
the of the scene illuminant. Such a method
has been proposed by a number of different authors [10,11,7,2].
An alternative, but related approach, was suggested by Lee et
al [8].
He proposed that we look not at values
but rather at their projection in a 2-d chromaticity space such as the 
space defined by:
 |
(3) |
In this case chromaticity co-ordinates can again be split into a linear
combination of the chromaticity corresponding
to surface reflectance (and thus the illuminant) and that corresponding to
body reflectance:
 |
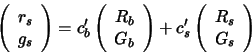(4) |
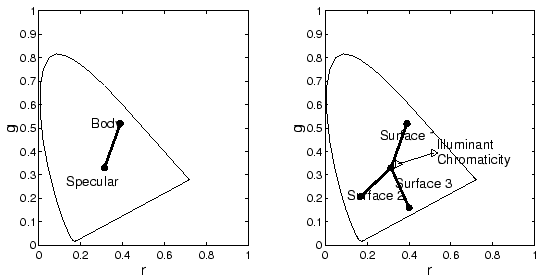
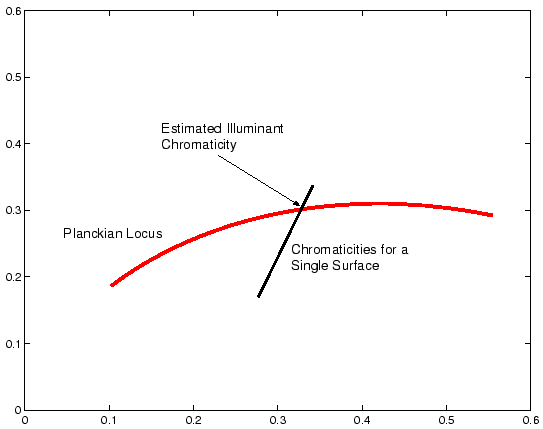
Equation 4 implies that chromaticity co-ordinates corresponding to a single surface will fall on a line in the 2-d space as illustrated in Figure 2. Co-ordinates for pixels corresponding to a second surface will fall on a second distinct line, pixels for a third surface fall on a third line and so on. Once again the intersection of the two or more lines identifies the illuminant: in this case in terms of its chromaticity co-ordinate.
|
Intersecting planes (in space) or lines (in chromaticity space) gives a
theoretically sound way to
discover the scene illuminant. However the algorithms rely, for their success,
on being able to reliably
distinguish pixels corresponding to a single surface. What is more, they
require at least two surfaces to be able
to operate at all. In our research we set out to remove the second of these
restrictions and to derive a physics
based algorithm which can estimate the scene illuminant given an image
consisting of only a single surface.
Our method works by incorporating prior knowledge of the physical nature of
the world into Lee's framework
for illuminant estimation. Specifically we enforce constraints on the set of
plausible illuminants which might
be encountered in the world. Figure 3 illustrates the chromaticity of a wide
range of illuminants which
occur in the world. It is clear that most of these lights are clustered around
the red line drawn
in this figure. This line represents the Planckian Locus: it represents the
chromaticity co-ordinates
of all blackbody radiators whose SPDs can be determined from the following
equation:
 |
(5) |
is a free parameter corresponding to the colour
temperature
of the source. By varying this parameter we can derive a range of spectral
power distributions such as those
shown in Figure 4. The projection of these spectra into chromaticity space
gives the Planckian locus.
 |
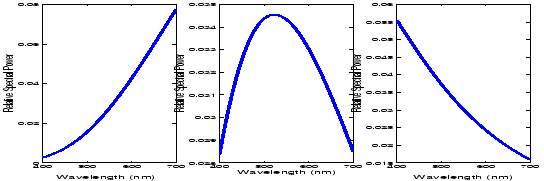Now suppose that we restrict illuminants to those which fall on the Planckian locus and consider an image of a single surface under some arbitrary illuminant. Following Lee et al all pixels in this image will project to a line in chromaticity space which has the form of Equation 5. It follows that we can identify the scene illuminant by intersecting the line of image chromaticities with the Planckian locus thus defining a method for estimating a scene illuminant which relies only on a single surface. Figure 5 illustrates the principal of the algorithm and Figure 6 shows an example of the algorithm's performance on an image of a single green plant. The left-hand image shows the raw image captured by a camera and the right-hand image shows the image corrected using an estimate of the scene illuminant obtained by the method set out above.
|
|
That we can solve for an estimate of the scene illuminant given the simplest scene content possible: a single surface, is a satisfying theoretical result. However, most scenes have a more complex structure than this and so we would like to extend our method to deal with the more common case of scenes with many surfaces. We would also like to relax the constraint that illuminants must lie on the Planckian locus and allow a wider range of non-Planckian lights to be considered. We consider first the relaxation on the illumination constraint. Looking again at Figure 3 which shows the chromaticities of a wide set of measured illuminant spectra we see that a more accurate representation of these plausible lights is a small subset of chromaticity space. We propose as others have done previously [3,5] to model this set by the convex hull of the points as illustrated by Figure 7. Now, we argue that any chromaticity in this set might correspond to an illuminant.
|
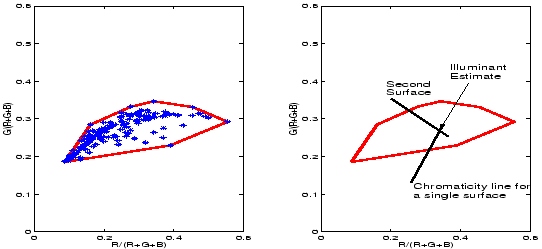
Extending
the algorithm to deal with multiple surfaces implies that we must be able to
segment our image into regions corresponding
to different surfaces. Suppose for the moment that such a segmentation is
attainable. Then we know that pixels belonging
to a single surface must fall on a line in chromaticity space (or a plane in
space). The right-hand plot of Figure 7 illustrates
that a line corresponding to a single surface intersects the set of possible
illuminants and so restricts the feasible illuminants to
the line segment which lies within the set. Adding a second surface, in theory
identifies the illuminant exactly: the lines from
the surfaces intersect at a point which falls within the set of possible
illuminants. In practice this ideal case might not occur: we have
many surfaces whose chromaticity lines may not all cross at a single point and
moreover, this point may fall outside the set
of possible lights. To deal with these practical difficulties we pose the
problem as an optimisation such that we wish to determine
the point which best represents the intersection of all chromaticity lines and
which is further constrained to fall within the
set of possible illuminants. It turns out that the necessary optimisation
belongs to a class of problem which is called Sequential
Quadratic Programming [6]: essentially we minimise a quadratic error
function subject to a set of linear and quadratic
constraints.
To complete the algorithm it remains to specify how a scene should be
segmented. Accurate segmentation of image data is very
difficult to achieve but we have found that our algorithm is robust to even
large inaccuracies in the segmentation. In fact, we have
found that very good results can be achieved even using a very naive
segmentation in which we simply divide the image into a number
of small sub-images. If a sub-image corresponds to a single surface its s
ought to lie on a plane in space. If they do not,
we reject this sub-block and in this way obtain a set of blocks which usually
correspond to single surfaces.
In other work on this method we have experimented with representing the set
of possible illuminants not by its convex hull but
using an 
-shape [1] representation which we have found further
improves accuracy. Work is ongoing to obtain a more
robust segmentation of the scene and to also combine this physics based
approach with statistical techniques for estimating
the scene illuminant which have also been developed in the
group [5,4].
on this method to further improve the seg
