, 
, and 
(or just
) and the response of a device to light from a point in a scene is a
triplet of numbers.
Mathematically these responses are related to light, surface, and sensor, thus:
Colour is a useful cue in helping us to recognise or identify an object. For this reason, faced with the problem of designing a computer that can recognise objects, vision researchers have considered how colour might help to achieve this task. More recently, a lot of research has concentrated on the related problem of image retrieval - how to identify images, similar in some way to a query image, from amongst a large database of images, perhaps on the web, or in some dedicated image archive. Once again, the use of colour has received considerable interest in this regard. While there is good evidence [10] to support the belief that colour is a useful aid in such tasks, there are a number of well documented limitations of indexing on colour alone.
Chief amongst these limitations is the fact that an object's colour is not an intrinsic property of the object itself, but rather it depends also on the conditions under which the object is viewed and on the properties of the device (or observer) that is viewing the object. For example, the light reflected from an object depends on properties of the object itself and also on the light which is incident upon it. A change in this incident light changes the ``colour'' that an object is recorded to be. It is easy to demonstrate [8,1] that if factors such as these are not taken into account, colour based recognition can fail dramatically.
In the Colour Group we are investigating ways to solve this problem. Our approach is to look for transformations of ``colour'' which are invariant to, for example, a change in illumination and to use this invariant information as our cue to help recognise the object. Our work has led to many different colour invariant features: a basic outline of each is given below.
To help us derive stable colour based features it is important that we
understand how ``colour'' arises in the first place. That is, we need an
understanding of the image formation process. We model image formation
as a process involving the interaction of three factors: light, surface, and
observer (a human observer or an imaging device such as a camera). Figure 1 illustrates
the nature of this interaction: light from a source is incident on a surface, is
reflected by that surface and the reflected light enters the imaging device.
Typically imaging devices sample the incoming light using three sensors,
preferentially sensitive to long (red), medium (green), and short (blue)
wavelength light. These responses are denoted by , , and (or just
) and the response of a device to light from a point in a scene is a
triplet of numbers.
Mathematically these responses are related to light, surface, and sensor, thus:
 |
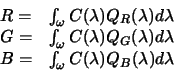(1) |
where 
is a function of wavelength 
characterising how a
given image sensor responds to the incident colour signal 
. The
colour signal is itself the product of the light incident upon a surface
(denoted 
) and the reflecting properties of the surface,
characterised by its surface reflectance function 
.
|
In fact Equation (1) is a very much simplified model of the image formation
process, but one which suffices on many occasions. The model can be made a
little more general by considering the fact that in general, the light reflected
from a surface depends on the angle of the surface with respect to the light
surface. Modelling this dependence
on geometry is quite straightforward: the intensity of the reflected light
depends on the cosine of the angle between the surface normal (a vector denoted
) and the angle of incidence of the light (a vector denoted 
).
The image formation equation then becomes:
 |
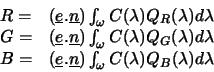(2) |
Equation (2) tells us that when the surface/lighting geometry changes, sensor
responses change by the same scale factor:
.
That is, the sensor responses to a surface seen under two different lighting
geometries are related by:
 |
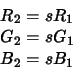(3) |
It is thus straightforward to remove the dependence of sensor responses on
lighting geometry. For example, we can simply divide responses by the sum of the
, , and responses:
 |
(4) |
The co-ordinates 
(commonly referred to as chromaticity
co-ordinates) are the simplest example of colour invariant
co-ordinates - they are invariant to changes in lighting geometry and also to
an overall change in the intensity of the incident light. Figure 2 illustrates
the effect of applying a chromaticity transform to an image. In the left-hand of
the figure it is clear that the light reflected from a point depends on the
position of the point with respect to the light source. Applying a chromaticity
transform leads to the right-hand image where this shading effect is removed.
|
A more challenging problem is to derive a set of features which are invariant to
a change in illumination colour - that is, we would like features which are
stable regardless of the illuminant spectral power distribution .
An inspection of the image formation equation (Equation 1) reveals why this is
a difficult problem: the illumination and the surface reflectance
are confounded in the formation of the response and it is thus non-trivial to
separate them.
Fortunately however, it is often the case that the relationship between sensor
responses under different illuminants can be explained by quite a simple model. In
particular model the sensor responses to a single surface viewed under two
different lights (which we denote (
and 
) can in many situations be modelled
as:
 |
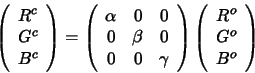(5) |
The diagonal model of illumination change tells us that corresponding pixels in two
images of the same scene under a pair of illuminants are related by three fixed
scale factors. For example, any red pixel image under light is related to its
corresponding pixel value under light by the factor 
. Now, suppose we
represent the image under illuminant by an 
matrix 
: each row of 
corresponds to an
image pixel. Then, the first column of is a vector containing all the red pixel
values in the image. Likewise the second and third columns are vectors containing
all green and all blue pixel values. Let us denote these vectors as
, 
, and 
so that we can then denote
the image as:
 |
(6) |
can be
written as:
 |
(7) |
assuming a diagonal model of illumination change. Interpreting , , and
as vectors in an 
-dimensional space (where corresponds to
the number of image pixels) then Equation 7 makes it clear how these three vectors
change with a change in illumination. The vector changes by a scale
factor : that is the length of the vector changes but its direction remains
constant (the vector grows longer or smaller according to whether is
greater than or less than one). Importantly the direction of the vectors do not
change with illumination - they are illumination invariant.
In early work on illumination invariance [3], members of the Colour Group have shown how the invariance of these vector directions can be used a cue to identify objects or images. Specifically, since the invariance of the vector directions imply that the angle between the red (r), green (g) and blue (b) vectors remain constant despite a change in illumination. Thus, if we represent an image by these vectors rather than by raw pixel values, we have an illumination invariant measure by which to summarise the image.
Experiments on image data have shown some success using this method, but it is not without problems. First amongst these problems is the fact that we are attempting to represent a complex image with many pixels with very few (just three) colour angles. In practice, three numbers are insufficient to reliably distinguish between a large number of images.
To address some of the shortcomings of the Colour Angles approach we have
considered alternative illuminant invariant methods. A second approach developed
by members of the group relies once again on a diagonal model of illumination
change. Suppose we have two neighbouring pixels imaged under an illuminant and
let us denote the sensor responses as:
and
. Under a change of illuminant these sensor
responses become
and
. Now consider what happens
if we take ratios of the responses at neighbouring pixels under the two different
lights. Under the first light (light ) we have ratios:
 |
(8) |
) we have:
 |
(9) |
From Equation (9) it is clear that when taking ratios, the scale factors ,
, and 
cancel out so that under both illuminants the ratios are the
same. That is, ratios of neighbouring pixels are again illumination invariant. Of
course, if the neighbouring pixels correspond to a single surface, then the ratios
are all unity and the so the ratios contain no useful information about the image.
However, at the edge between two surfaces, the pixel values are changing and so the
ratio values are no longer unity. Thus, ratios at pixels corresponding to the
boundary between surfaces convey some information about the two surfaces. Moreover,
if we form a histogram of these ratios (that is we count the number of times ratios
of a certain value occur in an image) we obtain a summary of colour information in
the image and that information is
also invariant to a change in illumination.
We have shown [9] that representing an image by a histogram of these ratio co-ordinates can lead to good object recognition/image retrieval even under changes in illumination. But the colour angles approach too has limitations. Chief amongst these is the fact that ratios can be unstable when the image contains noise - particularly in the case that the pixel values are small. That is, a small change in a pixel value can lead to a large change in the corresponding ratio. In addition, the ratios are invariant to a change in illumination colour, but not to a change in lighting geometry. Ideally we would like invariance to both.
In a third strand to our colour invariance research we have developed a
procedure to produce an image which is invariant to changes in both
illumination colour and lighting geometry. To understand this approach let us
once again represent an image of a scene under a light by an 
matrix with the rows of corresponding to the responses at each
pixel in an image:
 |
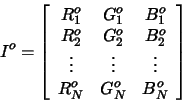(10) |
which
can be written:
 |
(11) |
, , and model the change in illumination
and the factors
account for the change in lighting geometry.
We have seen that dividing each sensor response at a pixel by the sum of the red,
green and blue responses at that pixel brings invariance to lighting geometry. We
can similarly achieve invariance to illumination colour by dividing the red sensor
response at a pixel by the mean of all red sensor responses, and similarly for
green and blue responses. Mathematically we can write this as:
 |
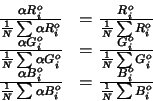(12) |
So, if we want to be invariant to lighting geometry, we divide the elements
of each row by
the sum of all elements in the row and if we want invariance to illumination colour
we divide the elements of each column by the mean of all column elements.
How then can we achieve invariance to both lighting geometry and illumination colour? An examination of the mathematics reveals that if we apply each of these processes one after the other, the invariant properties break down. However, we have been able to prove [4] that if we apply these two processes iteratively, two useful properties emerge. First, it can be shown that this iterative normalisation procedure converges to a fixed point and what is more this fixed point is independent of both illumination colour and lighting geometry.
|
This iterative procedure which we call Comprehensive Image Normalisation has a number of nice properties. First unlike our earlier invariant procedures, this procedure returns an image - that is we retain information at each pixel in the image as Figure 3 illustrates. This figure shows five input images, taken under five different illuminants and below each the comprehensively normalised image. The illumination invariance is demonstrated by the fact the resulting normalised images are very similar. We have shown that representing the information in these normalised images in histogram form, we are again able to achieve good indexing/recognition performance across illumination.
Comprehensive image normalisation is an iterative procedure. In recent work we have built upon the approach by formulating an alternative solution which is non-iterative, and which in addition to illumination colour and lighting geometry invariance, also provides invariance to gamma. More details of that work can be found in [6,2].
All the invariant features we have derived so far share one feature in common: they use information from all pixels in the image to construct colour invariant features. For example, comprehensive image normalisation works by dividing each pixel response by the mean of all pixel responses and producing invariant information at each pixel. More recently we have been addressing the problem as to whether or not it is possible to construct an illumination invariant feature at a pixel using only information contained at that pixel. If we adopt the model of image formation set out above, then the answer to this question is no. However, we have shown that by making certain further assumptions about the world that such per-pixel invariant information is obtainable. Further details of this work can be found here.